○ 円形 と 座標系 etc 円形とは、中心座標から等距離 r を、360度分繋いだ図形です。 通常レンズの輪郭は、円形 (球面)です。即ちレンズ設計 (実光線追跡、幾何光学) は、 円の方程式と光線(直線) 等の方程式の交点を、計算することになります。 中心が原点 (0.0) の円の方程式 は、x^2 + y^2 = r^2 となります。(x = (r^2-y^2) ^ 0.5 ) ○ 円形 と 座標系 (曲率 etc) 球面レンズの曲率 r は、円の半径 mm で表示します。 レンズ径とその曲率が判れば、その深さ、及び座標等も計算出来ます。 深さの計算式は、r -((r^2-y^2) ^ 0.5) です。 口径 80mm F 8.0 ・ r1 = 315mm、像高 40mm の場合、 315 -((315^2-40^2) ^0.5) = 2.55mm です。 (例) 中心座標 (315.0) r1 = 315mm の作図 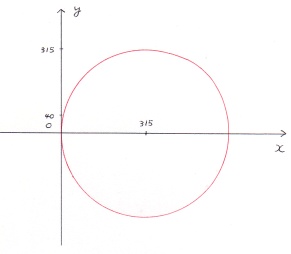 (方程式) ( x -315)^2 + y^2 = r^2 → y^2 = -x^2 +630x -315^2 + r^2 |
○ 円 と 微分、三角関数 etc 曲線の傾きは、微分することにより求められます。円の微分方程式は、-x/y です。 像高 40mm の場合、平行光線とレンズの交点の傾きは、(315-2.55)/40 = 7.81125 傾き →角度の変換は、atan 7.81125 = 82.70465 度 となります。 レンズの実光線追跡は、傾きの数値変換等を多用します。 三角関数 etc ○ レンズ設計値の表示 2枚玉対物レンズの場合、ガラス面は4面ありますので、設計値は、それぞれの曲率半径、 ガラスの種類、ガラスの中心厚、2枚玉間のスペースで表示します。 エアスペースは AIR 、バックフォーカス、約 630mm。 ガラスは、クラウンとフリントの2種に大別されます。(BK7.F2) 図面の左から、 r1 〜 r4 となります。 (左が光源、平行光) (密着式・アクロマートレンズ、データ 例) 口径 80mm F 8.0 (640mm) r1 = 315mm/9mm/BSL7 (BK7) r2 = -280mm/0.0mm/AIR r3 = -280mm/7mm/TIM2 (F2) r4 = -2100mm/630mm/AIR レンズ構成図 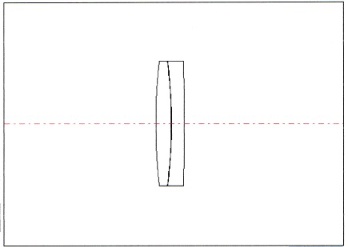 スネルの法則 etc |