△ 三角関数とは? 三角関数とは、傾き(角度) を求める関数です。微分方程式と組み合わせ、レンズ設計 が可能になります。 三角関数単独でも、測量等 ※で多用されます (斜辺傾き = 高さ/底辺 = y/x = TAN) 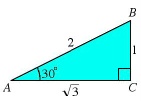 (備考) A 角度と 斜辺傾き (TAN)、一覧表
|
||||||||||||
○ 円 と 微分 曲線の傾きは、微分することにより求められます。円の微分方程式は、-x/y です。 r1 = 315mm、像高 40mm の場合、平行光線とレンズの交点の傾きは、(315-2.55)/40 = 7.81125 ※ (315 -((315^2-40^2) ^0.5) = 2.55) 傾き →角度の変換、atan 7.81125 = 82.70465 度 中心座標 (315.0) r1 = 315mm の作図 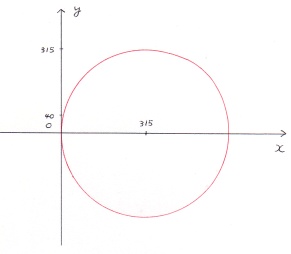 (備考) A 角度と 円接線 B の傾き(微分)、一覧表
|
||||||||||||
○ 微分と積分 (例) 重力による落下距離 1/2 gt^2 → 微分すると gt (加速度) 重力による加速度 gt → 積分すると 1/2 gt^2 (落下距離) 1秒後の落下距離 1/2 9.8*1^2 ≒ 5m。 加速度 9.8*1m/s |
||||||||||||
○ レンズの光学計算 (例) カメラレンズの画角計算 (35mmフルサイズ、36x24mm、対角線 43.2mm) 焦点距離 50mm の対角線画角 atan (43.2 x1/2)/50 ≒ 23.4 23.4 x 2 ≒ 46.8 度 画角一覧表 (35mmフルサイズ、対角線 )
|