仛丂傾僋儘儅乕僩丂懳暔儗儞僘愝寁 曽掱幃偵戙擖偟偰丄俀枃嬍丂傾僋儘儅乕僩懳暔儗儞僘偺愝寁乮嬋棪敿宎丂r1-倰4丂偺寛掕乯傪偟偰傒傑偡丅丂僈儔僗嵽偼俛俽俴俈乮俛俲俈乯丄俿俬俵俀乮俥俀乯丂傪巊梡偟傑偡丅乮峀媊偺乯僼儔儞儂乕僼僃儖宆乮儕僩儘乕宆乯丄嬋棪敿宎偺撪丄俀柺偺r2丄俁柺偺r3偼摨嬋棪偱愝寁偟傑偡丅 丂僗億僢僩丂etc 乮婎慴僨乕僞乯丂 俛俲俈丂丂丂値d丂1.5163丂丂丂倴d丂64.14丂丂撌儗儞僘丂丂丂乮倖1,n1,倴1乯 俥俀丂丂丂丂値d丂1.6200丂丂丂倴d丂36.25丂丂墯儗儞僘丂丂丂乮倖2,n2,倴2乯 岥宎丂俉侽倣倣丂徟揰嫍棧丂俇係侽倣倣丂乮俥俉乯 乮儕僩儘乕岞幃乯 f1丂=丂((v1-v2)xf)/v1 f2丂=丂((v1-v2)xf/v2 r1丂=丂2(n1-1)xf1 r2丂=丂-r1丂 倰3丂=丂r2丂 r4丂=丂1/(((1/r3)-(1/((n2-1)xf2)))) f1丂=丂((64.14-36.25)x640)/64.14丂=丂278.3 f2丂=丂((36.25-64.14)x640/36.25丂=丂-492.4 r1丂=丂2(1.5163-1)x278.3丂=丂+287.4 r2丂=丂-r1丂=丂-287.4 倰3丂=丂r2丂=丂-287.4 r4丂=丂1/(((1/-287.2)-(1/((1.6200-1)x-492.4))))丂=丂-4893 丒丒丒丂扨埵丂儈儕丄偲側傝傑偡丅 乮僄僋僙儖帺摦寁嶼僔乕僩乯 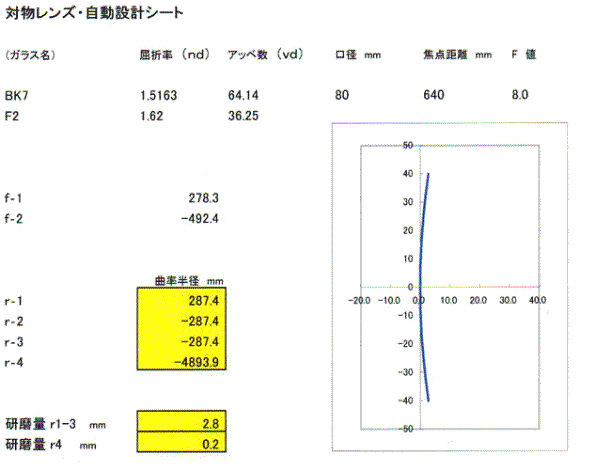 仛丂俀枃嬍儗儞僘偺岝慄捛愓仌媴柺廂嵎恾偺嶌惉 僗僱儖偺朄懃偲嶰妏娭悢丄旝暘丄擇師娭悢楢棫曽掱幃摍傪巊偭偨丄屆揟揑側幚岝慄捛愓僔儈儏儗乕僔儑儞偱偡丅儗儞僘慜柺偺拞怱偺嵗昗傪乮0,0乯偲偟偰寁嶼偟傑偡丅 奺嵗昗傪弴師寁嶼偟傑偡丅 嵗昗丂俙丂丂擖幩岝慄偲儗儞僘侾柺偲偺岎揰 丂丂丂伀 嵗昗丂俛丂丂擖幩岝慄偲儗儞僘俀丒俁柺偲偺岎揰 丂丂丂伀 嵗昗丂俠丂丂擖幩岝慄偲儗儞僘係柺偲偺岎揰 丂丂丂伀 嵗昗丂俢丂丂擖幩岝慄偲偺儗儞僘幉慄偲岎揰 嵗昗丂俢偺丂倶抣偑丄儗儞僘宯偺慡挿倢丂偲側傝傑偡丅乮僶僢僋僼僅乕僇僗亄僈儔僗岤傒乯 乮僶僢僋僼僅乕僇僗亄屻懁庡揰丂亖徟揰嫍棧偱偡丅乯丂 擖幩岝慄偺妏搙偼僛儘佮暯峴岝偲偟傑偡丅 |
 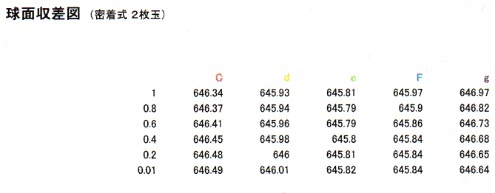 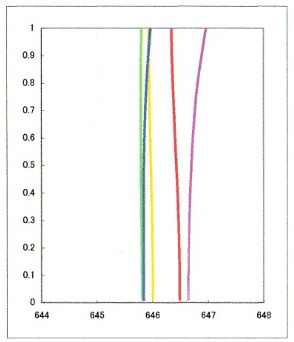 |
儕僩儘乕岞幃偱寁嶼偝傟偨嬋棪敿宎丂(r1-倰4乯媦傃僈儔僗庬暿丄岤傒丄僄傾僗儁乕僗傪丄乮帺嶌乯岝妛昡壙僜僼僩偵擖椡丄媴柺廂嵎恾傪弌椡偝偣傞偲丄嵍偵孹偄偨乮儅僀僫僗嵗昗懁偺乯廂嵎嬋慄偵側傞偙偲偑懡偄偺偱丄捈棫偡傞傛偆偵廋惓偡傞偙偲偑昁梫偵側傝傑偡丅倰2丂=丂倰3丂偺嬋棪偼摨堦偺傑傑丄丂r1丒倰4丂偦傟偧傟偺嬋棪傪栚嶼偱旝挷惍偟偰偄偒傑偡乮儁儞僨傿儞僌乯 儁儞僨傿儞僌偼丄r1偺嬋棪傪彮偟偢偮戝偒偔丄倰4丂偺嬋棪傪彮偟偢偮彫偝偔偡傞偲丄媴柺廂嵎丄峏偵偼僐儅廂嵎偑尭彮偟傑偡丅傑偨尋杹偺岺掱忋丄倰4偺嬋棪偑戝偒偡偓傞偲丄惍宍傗徟揰嫍棧偺應掕偵巟忈偑弌傞偙偲傕偁傝傑偡偺偱丄堄幆揑偵彫偝偔偡傞偙偲傕昁梫偱偡丅 俠倓倕俥倗丂偺俆慄偺撪丄倓倕俥偺俁慄偑怓徚偟偵側傞傛偆偵挷惍偡傞偲丄惎塤惎抍娤朷梡仌捈徟揰嶣塭梡偵側傞戙傢傝偵丄C慄偼傗傗塃懁乮僾儔僗嵗昗懁乯偵巆傝傑偡丅倗慄丄僐儅廂嵎傕傗傗巆傝傑偡丅 僐儅廂嵎偼丄惓尫忦審乮俷俽俠乯傛傝丄(h/sin)-倖丂偱媮傔傜傟傑偡丅倕慄婎弨偱憸崅倛=侾(40mm)丂偺応崌丄 乮40/0.062475乯-638.99丂佮丂1.26mm丂偺僐儅廂嵎偲側傝傑偡丂乮倳偼棧嶶妏丄atan(40/638.99)=3.5819搙乯 巇忋偘偲偟偰丄旝挷惍屻偵僘儗偨徟揰嫍棧傪僗働乕儕儞僌挷惍偟傑偡丅僗働乕儕儞僌偼丄徟揰嫍棧偺嵎堎棪傪丄奺嬋棪偵忔偠傑偡丅 姰惉僗儁僢僋偼丄埲壓偺捠傝偱偡丅 乮枾拝幃乯 r1丂=丂315mm/9mm/BSL7 (BK7) r2丂=丂-280mm/0.0mm/AIR 倰3丂=丂-280mm/7mm/TIM2 (F2) r4丂=丂-2100mm/630mm/AIR 乮暘棧幃 丂亄揤捀僾儕僘儉乯 r1丂=丂315mm/9mm/BSL7 (BK7) r2丂=丂-280mm/0.2mm/AIR 倰3丂=丂-280mm/7mm/TIM2 (F2) r4丂=丂-2100mm/570mm/AIR r5丂=丂丂丂丂0mm/30mm/BSL7 (BK7) r6丂=丂丂丂丂0mm/40mm/AIR 儗儞僘峔惉恾 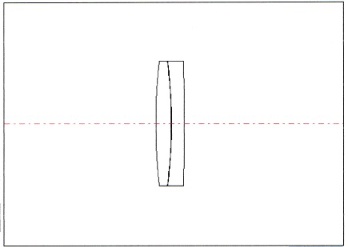 懳暔儗儞僘尋杹 |